Het geheim van de gulden snede

Vreemde rij

In 1202 publiceerde Leonardo Fibonacci een bijzondere rij getallen: elk getal van de rij (behalve de eerste twee) is gelijk aan de som van de twee voorgaande getallen. Dat levert de volgende rij getallen op: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, enzovoorts. De Fibonacci-reeks zit vol met eigenaardigheden, zoals elke optelsom van tien opeenvolgende getallen uit de reeks is deelbaar door elf (probeer maar eens). Om de zestig getallen herhaalt het laatste cijfer, bijvoorbeeld het tweede getal is 1, het tweeënzestigste getal in de reeks eindigt op een 1 (….4052739537881), het 122ste getal in de reeks eindigt op een ….. 1 (…..14028366653498915298923761), etcetera.

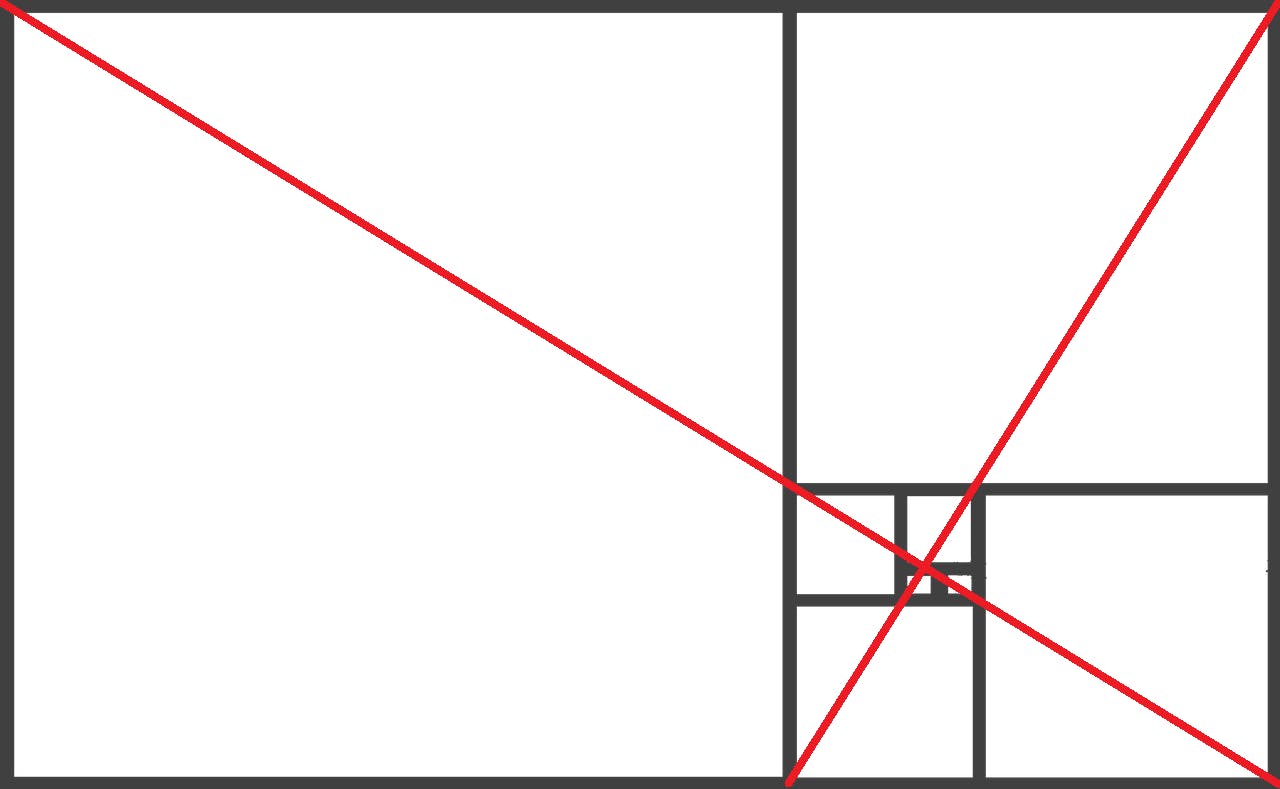
Het snijpunt van de diagonalen van alle rechthoeken werd in de renaissance het ‘Oog van God’ genoemd. De rechthoeken verkleinen zich volgens Φ.
Bron: TJ

Wonderlijke spiraal

Deze logaritmische spiraal komt in de natuur veelvuldig voor. Deze wonderlijke spiraal (Spiralis Mirabilis) wordt ook wel de Spiraal van Archimedes genoemd. Archimedes was helemaal gebiologeerd door spiralen en schreef er zelfs een compleet boek over. Veel slakkenhuizen zijn volgens dit patroon opgebouwd. Ook de hoorns van bijvoorbeeld een ram volgen dit patroon, maar ook sterrenstelsels. Uit figuur 5 blijkt dat de Spiralis Mirabilis rechtstreeks uit Φ is afgeleid. Kunstenaars maken veelvuldig van de spiraal gebruik. In de krullen van Leda, op het schilderij Leda en de zwaan van Leonardo da Vinci kun je ook de Spira mirabilis vinden.

Uit de verkleiningsreeks van deze rechthoeken volgens de verhouding Φ komt ook een spiraal.

Schilderkunst

De gulden snede komt dus veelvuldig voor in de natuur. Maar het belang van het getal is volgens sommigen nog veel groter. Zo was er de Italiaan Pacioli (1445- 1517) – een wiskundige kloosterling – die dacht dat schilderijen realistischer werden als de schilder de wetten van de wiskunde gehoorzaamt. Diepte in een schilderij, de verdeling van ruimtelijke vlakken over het linnen, liggen volgens Pacioli allemaal vast in wiskundige verhoudingen zoals Φ. Hij schreef drie boeken (bekend onder de naam ‘De Divina Proportione’) waarin hij de schilderkunst tot wiskundige figuren en vergelijkingen probeerde terug te brengen. Pacioli’s ideeën worden ook in recente tijden nog gebruikt: de abstracte kunst met gekleurde vlakken en lijnen van Mondriaan gebruikt bewust dan wel onbewust de gulden snede.

Muziek en Fibonacci

Ook andere kunsten zien de gulden snede langskomen. De muziekkunst kan bijvoorbeeld niet zonder de beroemde Fibonacci-reeks. De opbouw van de pianotoetsen volgt de reeks. Een octaaf op een piano wordt gespeeld met 8 witte toetsen en 5 zwarte, in totaal dus 13 toetsen. De zwarte toetsen zijn verdeeld in twee en drie. Dus de Fibonacci-reeks: 2, 3, 5, 8, 13! Volgens sommigen te ver gezocht en gewoon toeval, maar anderen geloven er heilig in. Componisten zoals Bartók en Debussy hebben de Fibonacci-reeks (bewust of onbewust?) in hun werk verstopt.

Vitruviaanse figuur getekend door Leonardo da Vinci.

Uiterlijk

Niet alleen in de kunst kom je Φ tegen, ook menselijke schoonheid volgt de wetten van de gulden snede. In het menselijke gezicht vind je allerlei verhoudingen die de gulden snede benaderen. Bijvoorbeeld de verhouding van de lengte van je neus tot de breedte. Of de afstand tussen je ogen tot de totale breedte van je gezicht. Misschien verklaart het aantal gulden sneden die in het gezicht voorkomen, of iemand knap is of niet. Dus als je wilt weten of je een knappe vriend of vriendin aan de haak hebt geslagen, moet je op zoek naar de gulden snede in zijn of haar gezicht!

Dit gaat natuurlijk ver. Kan je iemands schoonheid kwantificeren, in een aantal gulden sneden uitdrukken? nee dat kan niet. Het is wel zo dat een verregaande symmetrie in het gezicht meestal aantrekkelijker is, en die symmetrie hangt mogelijk samen met de gulden snede. Er is veel onderzoek gedaan naar gezichtsverhoudingen en aantrekkelijkheid, maar elk onderzoek heeft andere resultaten: onomstotelijk bewijs dat een gulden gezicht beter is, is er dus niet.

Goddelijk?

De gulden snede bemoeit zich met natuur, muziek, schilderkunst en zelfs de menselijke schoonheid. Hoe kan het dat zo’n vreemd getal, bij benadering 1,62, zo een grote rol speelt? Daarover hebben wiskundigen, filosofen en kunstenaars lange tijd hun hoofd gebroken. In de Middeleeuwen en Renaissance was het een godsbewijs: dat zonnebloemen, mensen en muziek voldeden aan één en dezelfde regel, dat moest haast wel komen doordat god alles schiep met een vooropgezet plan. Zelfs nu gebruiken sommige creationisten – die evolutie afwijzen als verklaring voor het ontstaan van leven en de ontwikkeling van soorten – het argument nog.

De wetenschap heeft nog geen goede verklaring waarom de Fibonacci-reeks en gulden snede zo vaak bij planten en bloemen voorkomen. Eén van de verklaringen is dat deze verhoudingen de efficiëntste manier zijn om te groeien: met de minste energie zo groot mogelijk worden. Het zou verklaren waarom planten zo vaak dezelfde verhouding tonen. Waarom het dan precies de gulden snede is, waarin de bloemen zich verhouden, dat is lastiger uit te leggen.

Er is een andere, ietwat teleurstellende verklaring: toeval. Er zijn inderdaad veel dingen in de natuur die de gulden snede volgen, maar het is niet dé regel van de natuur. Voor elke bloem die de Fibonacci-reeks volgt, zijn er honderden die dat niet doen. Die misschien wel andere, minder bekende patronen volgen. Aangezien wetenschappers al eeuwenlang bezig zijn met de gulden snede en deze ook actief opzoeken in de natuur, treedt er een ‘confirmation bias’ op: het fenomeen dat je bewijs vindt voor datgene waar je naar zoekt. Je onthoudt de gevallen waar phi een rol speelt en vergeet de gevallen waar het niet zo was, of waar de benadering van de gulden snede minder sterk is. Zo kan een beeld ontstaat dat het getal óveral voorkomt, terwijl de realiteit anders is.

Deze lijn visualiseert de betekenis van Φ in de meetkunde. De verhouding van de lijnstukken AC/BC is gelijk aan de verhouding van de lijnstukken AB/AC.

Ten slotte een manier om zelf de gulden snede te ontdekken, en te kijken wat je er allemaal mee kan.

Het wiskundige probleem waar Euclidus mee stoeide is weergegeven in bovenstaande figuur. Als we een rechte lijn in twee stukken willen verdelen, hoe lang moeten de lijnstukken zijn om ervoor te zorgen dat de verhouding tussen het grootste lijnstuk (AC) en het kleinste lijnstuk (BC) gelijk is aan de verhouding tussen het gehele deel (AB) en het grootste lijnstuk (AC)? Een wiskundige zou de vraag als volgt opschrijven: waar ligt punt C op de lijn AB zodat geldt: AC/BC = AB/AC? Stel dat de lengte van lijnstuk BC gelijk is aan 1 en die van AC gelijk aan x. We weten dat AC/BC = AB/AC, dus invullen levert op: x / 1 = (x + 1) / x. Kruiselings vermenigvuldigen levert op: x² = x + 1, oftewel x² – x – 1 = 0. Deze kwadratische vergelijking is eenvoudig met behulp van de abc-formule op te lossen. Er zijn twee oplossingen: x₁ = (1 + √5)/2 en x₂ = (1 – √5)/2. Even narekenen op het rekenapparaatje en je zult zien dat x₁ het getal 1,618 oplevert! De waarde x₂ is negatief, dus deze voldoet niet als lengte van een lijnstuk. Hiermee hebben we met eenvoudige wiskunde het bewijs geleverd voor het bestaan van Φ. Lijnstuk AC is dus 1,618… keer zo lang als lijnstuk BC. En lijnstuk AB is 1,618… keer zo lang als lijnstuk AC. Lijnstuk AC is dus 1,618 en wordt aangeduid met de Griekse letter Φ.

Tik het getal van Φ nog eens in je rekenmachine in (dus: 1,6180339887); bereken vervolgens het kwadraat (x² op je calculator) en daarna de reciproke waarde (de 1/x knop op je calculator). Wat valt je op? Als je het goed gedaan hebt, veranderen de cijfers achter de komma niet, alleen het getal voor de komma.